深谷技术 | 基于牛顿-欧拉法的轮腿机器人动力学建模

       轮腿机器人是一种融合轮式移动高效性与腿式结构灵活性的复合型机器人，既可通过轮式结构在平坦地形实现高速运动与高能量利用率，又能借助仿生步态跨越障碍、攀爬斜坡，适应复杂地形。通过轮-腿模式的动态切换，兼顾了传统轮式机器人快速稳定的运动能力与足式机器人对崎岖环境的强适应能力，在工业自动化、灾难救援、物流配送等领域展现出广阔的应用潜力。

       轮腿式机器人独特的多模式运动能力带来了复杂的物理交互问题。研究其动力学特性对实现有效运动控制、提升稳定性和能量效率具有重要意义。

牛顿-欧拉法

       牛顿-欧拉法作为动力学中一种经典的多体系统建模方法，结合了牛顿的平动定律（F=maF=ma）与欧拉的转动定律（力矩与角加速度的关系）。在这种方法中，系统的状态由位置、速度和加速度来描述，因此需要确定系统的受力和力矩。牛顿-欧拉法直观易懂，适用于描述复杂系统的运动，在实际工程领域有广泛应用。

       本篇文章中，我们将建立两轮足式机器人加入机体俯仰角自由度的多自由度轮足倒立摆模型，将两轮足式机器人简化为驱动轮、摆杆和机体三部分，采用牛顿力学法分别对驱动轮、摆杆和机体进行受力分析建立其动力学模型。

轮足倒立摆简化模型如图1所示。图中各项物理参数见表1

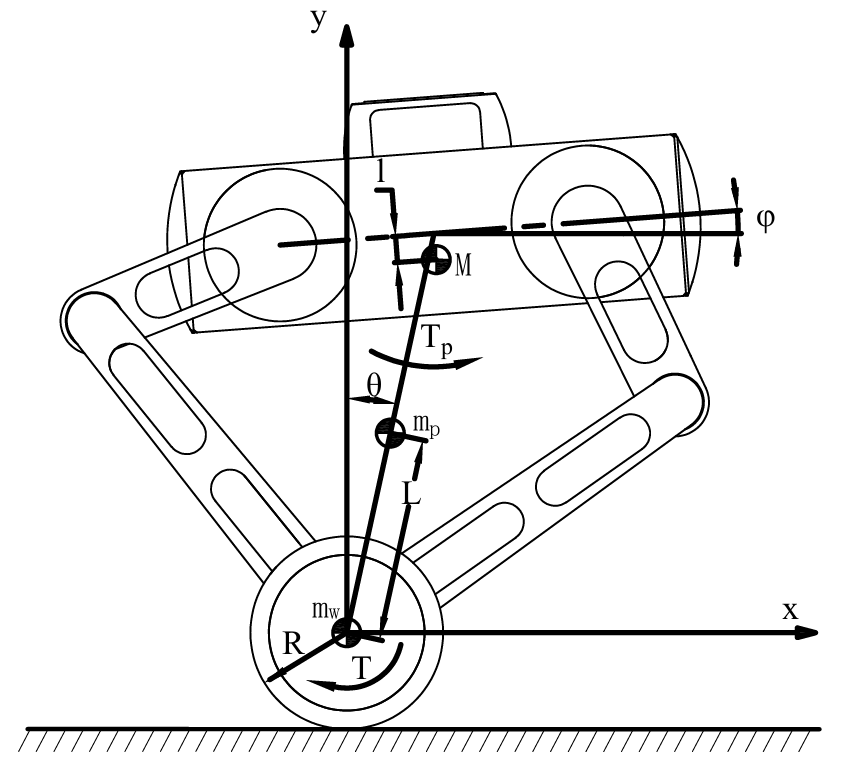
图1 轮足倒立摆简化模型

表1 轮足倒立摆模型各物理参数

     根据驱动轮电机给驱动轮施加的旋转力矩和摆杆给驱动轮施加的力以及驱动轮与地面的摩擦力，如图2所示。

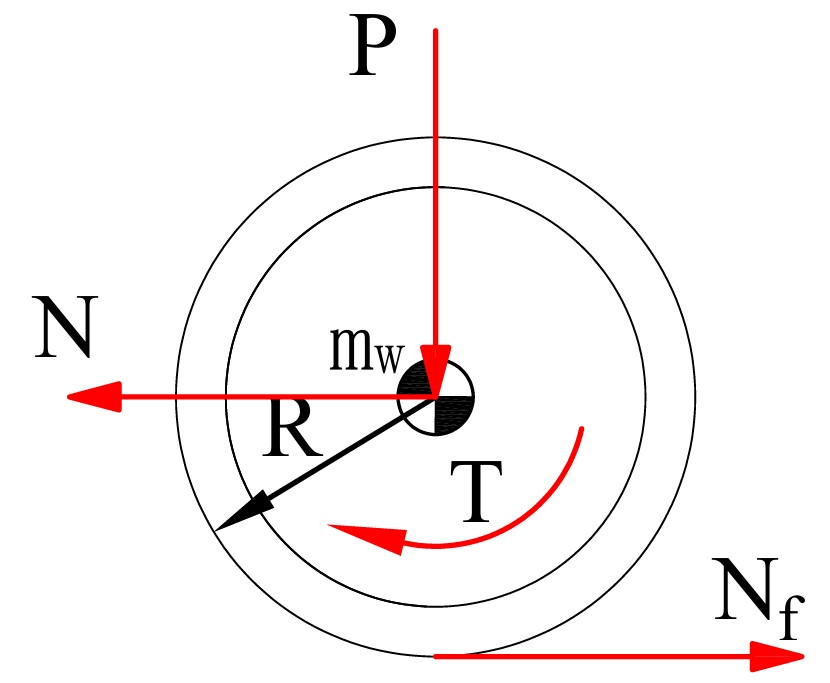
图2 驱动轮受力分析示意图

可得轮子的运动方程： 

水平方向上：

转动：

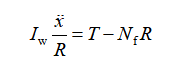
联立可得：

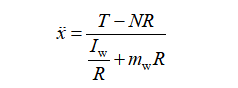
对摆杆分析有受到驱动轮施加的反作用力和力矩、机体施加的反作用力、自身重力和关节电机施加的摆杆侧摆力矩，如图3所示。

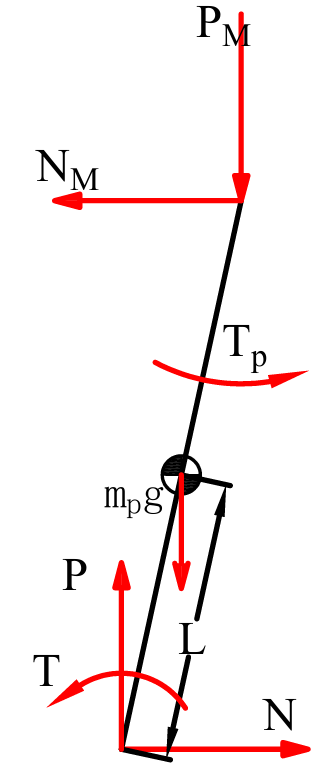
图3 摆杆受力分析示意图

则水平方向上：

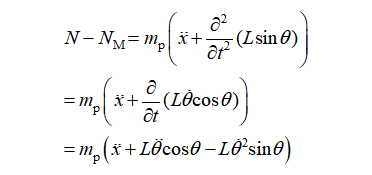
竖直方向上：

转动：

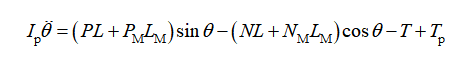
对机体分析有摆杆对机体的支撑力、自身重力和摆杆前摆的反作用力矩，如图4所示。

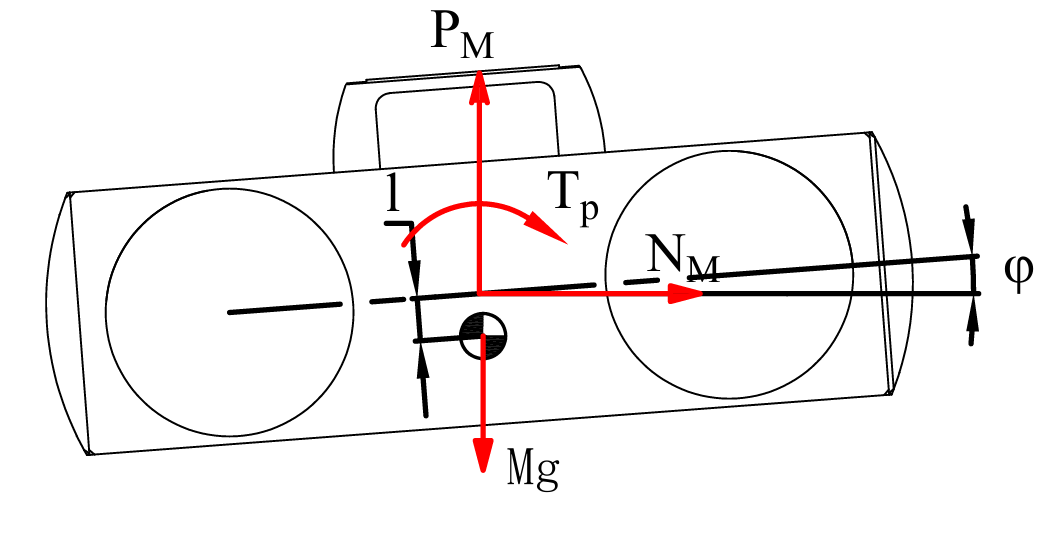
图4 机体受力分析示意图

则水平方向上：

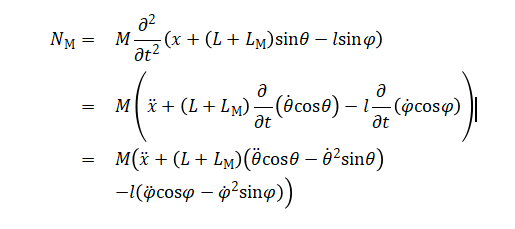
竖直方向上：

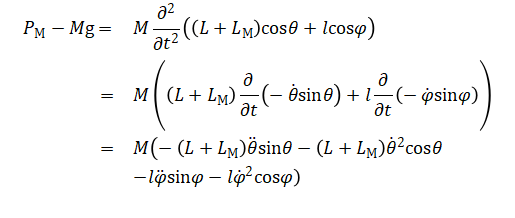
转动：

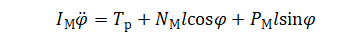
联立消去中间变量得：

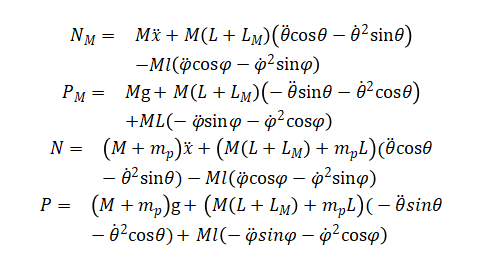
回代可得：

令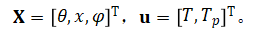

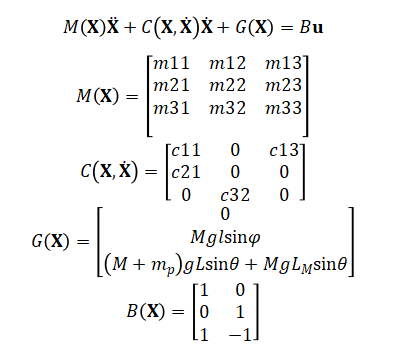
       经过上述的推导和分析，我们可以建立起轮腿机器人的动力学方程。

       轮腿动力学建模既揭示了复杂物理交互的本质，同时也为后续机器人控制算法的设计提供了关键数学支撑。以此为基石持续优化模型、改进算法，可推动轮腿机器人技术进一步发展，助力其在难救援、野外勘探、物流配送等更多领域发挥作用。